三道Crypto练习

0x00 pwnhub公开赛-sign_in_rsa

from Crypto.Util.number import getPrime, long_to_bytes, bytes_to_long, inverse
import math
from gmpy2 import next_prime

FLAG = b"flag{************************************************}"

p = getPrime(1024)
q = getPrime(1024)
N = p*q
phi = (p-1)*(q-1)
e = 0x10001
d = inverse(e, phi)

my_key = (N, d)

friends = 5
friend_keys = [(N, getPrime(17)) for _ in range(friends)]

cipher = bytes_to_long(FLAG)

for key in friend_keys:
    cipher = pow(cipher, key[1], key[0])

print(f"My private key: {my_key}")
print(f"My Friend's public keys: {friend_keys}")
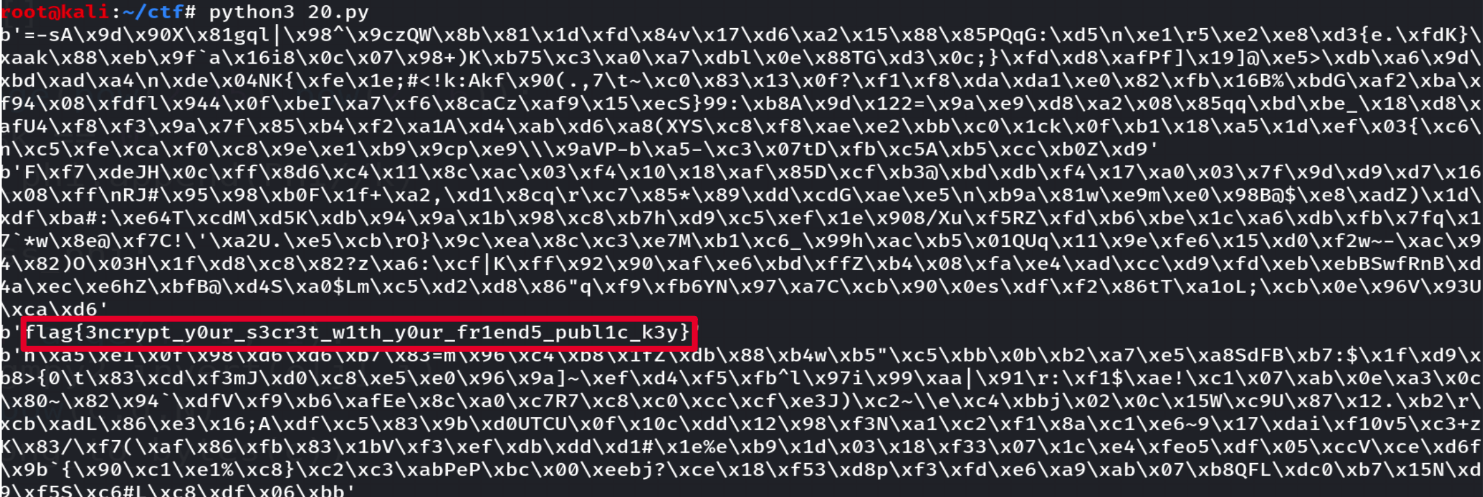
print(f"Encrypted flag: {cipher}")

首先分析代码在output.txt里面My private key表示N和D，My Friend’s public keys表示五组素数与N，然后是加密完的密文C。盘一下已知的数，E、N、D、C和五组素数。

原本的flag是将五组素数分别作为e，加密后得到密文的，所以需要倒推这个过程，然而N无法分解，但我们有E和D，E*D=k*(p-1)*(q-1)，这里把E*D设为PHI。我们知道N的位数是2046位，PHI的位数则是2061-2062位，也就是说k的取值范围在2的15次方和16次方之间。

编写脚本后可以发现k的取值只有四种可能：36906、55359、56774、61510。

最终脚本如下：

import gmpy2
from Crypto.Util.number import *

e = [107273,80021,110281,125399,77641]
PHI = D*E-1
poss_phi = []

for k in range(pow(2,15),pow(2,16)):
	if PHI %k == 0:
		poss_phi.append(PHI//k)
		
for i in poss_phi:
	c=C
	for j in range(4,-1,-1):
		d = gmpy2.invert(e[j],i)
		c = pow(c,d,N)
	print (long_to_bytes(c))

在输出中找到flag{3ncrypt_y0ur_s3cr3t_w1th_y0ur_fr1end5_publ1c_k3y}

0x01 已知p高位攻击

from secret import flag
from Crypto.Util.number import *

m = bytes_to_long(flag)

p = getPrime(512)
q = getPrime(512)
N = p * q
e = 7

c = pow(m, e, N)
high_p = (p >> 100) << 100

print(c, N, high_p, sep='\n')

从代码中可以看到，p的值经过了左移右移，得到的high_p，我们可以转换成16进制看一下，0xf1f642e6084bc092c008d07d821d5722fa98c5d424db505332622a1506e0d22d5e42d4d1025eb24e665f23b1e6041b6dd96705d0000000000000000000000000，可以发现后面全部是0，但高位已知，该后门算法依赖于Coppersmith partial information attack算法，sage代码如下：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13

n = 99887986204824691113457754897953425406993412586030259044004283966194202433452866024995465248688896193125819761385921365388030307691682145106269184432165936577174730773115650122496935533603059557681592007428920955897003476296682566264772005134125852663260971355535474414913501328212769545952135420770881499467
p = 12672576027810761975840956553905924324108169270520824932988309977042643967090398117355253953195633095326913407044418517938976916071656473263683948565757952

kbits = 100//kbit是未知的p的低位位数
PR.<x> = PolynomialRing(Zmod(n))//生成一个以x为符号的一元多项式环
f = x + p//定义求解的函数
x0 = f.small_roots(X=2^kbits, beta=0.4)[0]//多项式小值根求解及因子分解,X表示求解根的上界,x0为求出来的p低位
print ("x: %s" %int(x0))
p = p+x0
print ("p: ", int(p))
assert n % p == 0
q = n/int(p)
print ("q: ", int(q))

得到结果：

1
2
3

x: 389012076266827076910275508475
p:  12672576027810761975840956553905924324108169270520824932988309977042643967090398117355253953195633095326913407044418517938977305083732740090760858841266427
q:  7882216369080307573684148336656348276125777637863593106760322365174229732530885238209013585945585289415095195664039487452042451160318978844874180224833521

已知p、q后就是一个简单的解密过程了，最后得到结果flag {47b9332b7527b8905cc0a31c8496347e}

0x02 维纳攻击

from secret import flag
from Crypto.Util.number import *

m = bytes_to_long(flag)

p = getPrime(512)
q = getPrime(512)
N = p * q
phi = (p-1) * (q-1)
while True:
    d = getRandomNBitInteger(200)
    if GCD(d, phi) == 1:
        e = inverse(d, phi)
        break

c = pow(m, e, N)

print(c, e, N, sep='\n')

题目给出d的位数最大是200，N的位数是1022，绝对小于254位，这里用到https://github.com/orisano/owiener求解。

d = owiener.attack(e, N)

已知c,d,N即可解出flag。