## 0x00 [MRCTF2020]Easy_RSA
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
import sympy
from gmpy2 import gcd , invert
from random import randint
from Crypto.Util.number import getPrime , isPrime , getRandomNBitInteger , bytes_to_long , long_to_bytes
import base64
from zlib import *
flag = b "MRCTF {XXXX} "
base = 65537
def gen_prime ( N ):
A = 0
while 1 :
A = getPrime ( N )
if A % 8 == 5 :
break
return A
def gen_p ():
p = getPrime ( 1024 )
q = getPrime ( 1024 )
assert ( p < q )
n = p * q
print ( "P_n = " , n )
F_n = ( p - 1 ) * ( q - 1 )
print ( "P_F_n = " , F_n )
factor2 = 2021 * p + 2020 * q
if factor2 < 0 :
factor2 = ( - 1 ) * factor2
return sympy . nextprime ( factor2 )
def gen_q ():
p = getPrime ( 1024 )
q = getPrime ( 1024 )
assert ( p < q )
n = p * q
print ( "Q_n = " , n )
e = getRandomNBitInteger ( 53 )
F_n = ( p - 1 ) * ( q - 1 )
while gcd ( e , F_n ) != 1 :
e = getRandomNBitInteger ( 53 )
d = invert ( e , F_n )
print ( "Q_E_D = " , e * d )
factor2 = 2021 * p - 2020 * q
if factor2 < 0 :
factor2 = ( - 1 ) * factor2
return sympy . nextprime ( factor2 )
if __name__ == "__main__" :
_E = base
_P = gen_p ()
_Q = gen_q ()
assert ( gcd ( _E , ( _P - 1 ) * ( _Q - 1 )) == 1 )
_M = bytes_to_long ( flag )
_C = pow ( _M , _E , _P * _Q )
print ( "Ciphertext = " , _C )
'''
P_n = 14057332139537395701238463644827948204030576528558543283405966933509944444681257521108769303999679955371474546213196051386802936343092965202519504111238572269823072199039812208100301939365080328518578704076769147484922508482686658959347725753762078590928561862163337382463252361958145933210306431342748775024336556028267742021320891681762543660468484018686865891073110757394154024833552558863671537491089957038648328973790692356014778420333896705595252711514117478072828880198506187667924020260600124717243067420876363980538994101929437978668709128652587073901337310278665778299513763593234951137512120572797739181693
P_F_n = 14057332139537395701238463644827948204030576528558543283405966933509944444681257521108769303999679955371474546213196051386802936343092965202519504111238572269823072199039812208100301939365080328518578704076769147484922508482686658959347725753762078590928561862163337382463252361958145933210306431342748775024099427363967321110127562039879018616082926935567951378185280882426903064598376668106616694623540074057210432790309571018778281723710994930151635857933293394780142192586806292968028305922173313521186946635709194350912242693822450297748434301924950358561859804256788098033426537956252964976682327991427626735740
Q_n = 20714298338160449749545360743688018842877274054540852096459485283936802341271363766157976112525034004319938054034934880860956966585051684483662535780621673316774842614701726445870630109196016676725183412879870463432277629916669130494040403733295593655306104176367902352484367520262917943100467697540593925707162162616635533550262718808746254599456286578409187895171015796991910123804529825519519278388910483133813330902530160448972926096083990208243274548561238253002789474920730760001104048093295680593033327818821255300893423412192265814418546134015557579236219461780344469127987669565138930308525189944897421753947
Q_E_D = 100772079222298134586116156850742817855408127716962891929259868746672572602333918958075582671752493618259518286336122772703330183037221105058298653490794337885098499073583821832532798309513538383175233429533467348390389323225198805294950484802068148590902907221150968539067980432831310376368202773212266320112670699737501054831646286585142281419237572222713975646843555024731855688573834108711874406149540078253774349708158063055754932812675786123700768288048445326199880983717504538825498103789304873682191053050366806825802602658674268440844577955499368404019114913934477160428428662847012289516655310680119638600315228284298935201
Ciphertext = 40855937355228438525361161524441274634175356845950884889338630813182607485910094677909779126550263304194796000904384775495000943424070396334435810126536165332565417336797036611773382728344687175253081047586602838685027428292621557914514629024324794275772522013126464926990620140406412999485728750385876868115091735425577555027394033416643032644774339644654011686716639760512353355719065795222201167219831780961308225780478482467294410828543488412258764446494815238766185728454416691898859462532083437213793104823759147317613637881419787581920745151430394526712790608442960106537539121880514269830696341737507717448946962021
'''
可以根据P_n和P_F_n的关系求出_P,此处有个小细节,p < q。
pqplus = P_n - P_F_n + 1
pqminus = gmpy2.isqrt(pqplus**2-4*P_n)
p1 = (pqplus-pqminus)//2
factor1 = 2020 * pqplus + p1
_P = nextprime(factor1)而_Q则可以通过,Q_E_D=e*d=k*phi+1=k*(p-1)*(q-1)+1=k*(p*q-(p+q)+1)+1=k*(n -(p+q)+1)+1=k*n- k*(p+q)+k+1,而这个值绝对小于k*n,所以,可以通过下面代码求出phi,进而求出_Q。
K = ((Q_E_D-1)//Q_n)+1
Q_F_n = (Q_E_D-1)//K0x01 [羊城杯 2020]RRRRRRRSA
import hashlib
import sympy
from Crypto.Util.number import *
flag = 'GWHT{************}'
flag1 = flag[:19].encode()
flag2 = flag[19:].encode()
assert(len(flag) == 38)
P1 = getPrime(1038)
P2 = sympy.nextprime(P1)
assert(P2 - P1 < 1000)
Q1 = getPrime(512)
Q2 = sympy.nextprime(Q1)
N1 = P1 * P1 * Q1
N2 = P2 * P2 * Q2
E1 = getPrime(1024)
E2 = sympy.nextprime(E1)
m1 = bytes_to_long(flag1)
m2 = bytes_to_long(flag2)
c1 = pow(m1, E1, N1)
c2 = pow(m2, E2, N2)题目给出了N1、c1、E1、N2、c2、E2的值,参考https://blog.csdn.net/a5555678744/article/details/117701126
原理里面提到了维纳攻击,这是依靠连分数进行的攻击方式,适用于非常接近某一值时,求一个比例关系,通过该比例关系再来反推关键信息。
对于这一道题:N1/N2=(P1/P2)**2 * (Q1/Q2),我们可以推断出N1/N2 <Q1/Q2,从而得到区间范围(N1/N2,1),尝试对N1/N2进行连分数展开并求其各项渐进分数,其中某个连分数的分母就是Q1。
from Crypto.Util.number import *
import gmpy2
def continuedFra(x, y): #不断生成连分数的项
cF = []
while y:
cF += [x // y]
x, y = y, x % y
return cF
def Simplify(ctnf): #化简
numerator = 0
denominator = 1
for x in ctnf[::-1]: #注意这里是倒叙遍历
numerator, denominator = denominator, x * denominator + numerator
return (numerator, denominator) #把连分数分成分子和算出来的分母
def getit(c):
cf=[]
for i in range(1,len(c)):
cf.append(Simplify(c[:i])) #各个阶段的连分数的分子和分母
return cf #得到一串连分数
def wienerAttack(e, n):
cf=continuedFra(e,n)
for (Q2,Q1) in getit(cf):#遍历得到的连分数,令分子分母分别是Q2,Q1
if Q1 == 0:
continue
if N1%Q1==0 and Q1!=1:#满足这个条件就找到了
return Q1
print('not find!')
Q1=wienerAttack(N1,N2)
P1=gmpy2.iroot(N1//Q1,2)[0]
P2=gmpy2.next_prime(P1)
Q2=gmpy2.next_prime(Q1)
phi1=P1*(P1-1)*(Q1-1)
phi2=P2*(P2-1)*(Q2-1)
d1=gmpy2.invert(E1,phi1)
d2=gmpy2.invert(E2,phi2)
m1=long_to_bytes(gmpy2.powmod(c1,d1,N1))
m2=long_to_bytes(gmpy2.powmod(c2,d2,N2))
print((m1+m2))0x02 [De1CTF2019]babyrsa
1
2
3
4
5
6
7
import binascii
from data import e1 , e2 , p , q1p , q1q , hint , flag
n = [ 20129615352491765499340112943188317180548761597861300847305827141510465619670536844634558246439230371658836928103063432870245707180355907194284861510906071265352409579441048101084995923962148527097370705452070577098780246282820065573711015664291991372085157016901209114191068574208680397710042842835940428451949500607613634682684113208766694028789275748528254287705759528498986306494267817198340658241873024800336013946294891687591013414935237821291805123285905335762719823771647853378892868896078424572232934360940672962436849523915563328779942134504499568866135266628078485232098208237036724121481835035731201383423 L , 31221650155627849964466413749414700613823841060149524451234901677160009099014018926581094879840097248543411980533066831976617023676225625067854003317018794041723612556008471579060428898117790587991055681380408263382761841625714415879087478072771968160384909919958010983669368360788505288855946124159513118847747998656422521414980295212646675850690937883764000571667574381419144372824211798018586804674824564606122592483286575800685232128273820087791811663878057827386379787882962763290066072231248814920468264741654086011072638211075445447843691049847262485759393290853117072868406861840793895816215956869523289231421 L , 29944537515397953361520922774124192605524711306753835303703478890414163510777460559798334313021216389356251874917792007638299225821018849648520673813786772452822809546571129816310207232883239771324122884804993418958309460009406342872173189008449237959577469114158991202433476710581356243815713762802478454390273808377430685157110095496727966308001254107517967559384019734279861840997239176254236069001453544559786063915970071130087811123912044312219535513880663913831358790376650439083660611831156205113873793106880255882114422025746986403355066996567909581710647746463994280444700922867397754748628425967488232530303 L , 25703437855600135215185778453583925446912731661604054184163883272265503323016295700357253105301146726667897497435532579974951478354570415554221401778536104737296154316056314039449116386494323668483749833147800557403368489542273169489080222009368903993658498263905567516798684211462607069796613434661148186901892016282065916190920443378756167250809872483501712225782004396969996983057423942607174314132598421269169722518224478248836881076484639837343079324636997145199835034833367743079935361276149990997875905313642775214486046381368619638551892292787783137622261433528915269333426768947358552919740901860982679180791 L ]
c = [ 19131432661217908470262338421299691998526157790583544156741981238822158563988520225986915234570037383888112724408392918113942721994125505014727545946133307329781747600302829588248042922635714391033431930411180545085316438084317927348705241927570432757892985091396044950085462429575440060652967253845041398399648442340042970814415571904057667028157512971079384601724816308078631844480110201787343583073815186771790477712040051157180318804422120472007636722063989315320863580631330647116993819777750684150950416298085261478841177681677867236865666207391847046483954029213495373613490690687473081930148461830425717614569 L , 15341898433226638235160072029875733826956799982958107910250055958334922460202554924743144122170018355117452459472017133614642242411479849369061482860570279863692425621526056862808425135267608544855833358314071200687340442512856575278712986641573012456729402660597339609443771145347181268285050728925993518704899005416187250003304581230701444705157412790787027926810710998646191467130550713600765898234392350153965811595060656753711278308005193370936296124790772689433773414703645703910742193898471800081321469055211709339846392500706523670145259024267858368216902176489814789679472227343363035428541915118378163012031 L , 18715065071648040017967211297231106538139985087685358555650567057715550586464814763683688299037897182845007578571401359061213777645114414642903077003568155508465819628553747173244235936586812445440095450755154357646737087071605811984163416590278352605433362327949048243722556262979909488202442530307505819371594747936223835233586945423522256938701002370646382097846105014981763307729234675737702252155130837154876831885888669150418885088089324534892506199724486783446267336789872782137895552509353583305880144947714110009893134162185382309992604435664777436197587312317224862723813510974493087450281755452428746194446 L , 2282284561224858293138480447463319262474918847630148770112472703128549032592187797289965592615199709857879008271766433462032328498580340968871260189669707518557157836592424973257334362931639831072584824103123486522582531666152363874396482744561758133655406410364442174983227005501860927820871260711861008830120617056883514525798709601744088135999465598338635794275123149165498933580159945032363880613524921913023341209439657145962332213468573402863796920571812418200814817086234262280338221161622789516829363805084715652121739036183264026120868756523770196284142271849879003202190966150390061195469351716819539183797 L ]
f = lambda m , e , n , c : pow ( m , e , n ) == c
assert ( sum ( map ( f ,[ p ] * 4 ,[ 4 ] * 4 , n , c )) == 4 )
第一部分给出了四组n和c,这里想到低加密指数广播攻击,p是lanbda中的m,e是4,这里可以先求出p的值。
import gmpy2
from Crypto.Util.number import *
#利用中国剩余定理求解同余方程,aList:余数,mList:模数
def CRT(aList, mList):
M = 1
for i in mList:
M = M * i #计算M = ∏ mi
#print(M)
x = 0
for i in range(len(mList)):
Mi = M // mList[i] #计算Mi
Mi_inverse = gmpy2.invert(Mi, mList[i]) #计算Mi的逆元
x += aList[i] * Mi * Mi_inverse #构造x各项
x = x % M
return x
x = CRT(c, n)
p = gmpy2.iroot(x, e)[0] #对x开e次根
print(p)得到109935857933867829728985398563235455481120300859311421762540858762721955038310117609456763338082237907005937380873151279351831600225270995344096532750271070807051984097524900957809427861441436796934012393707770012556604479065826879107677002380580866325868240270494148512743861326447181476633546419262340100453
第二部分是低加密指数攻击
1
2
3
4
5
6
7
8
ee1 = 42
ee2 = 3
ce1 = 45722651786340123946960815003059322528810481841378247280642868553607692149509126962872583037142461398806689489141741494974836882341505234255325683219092163052843461632338442529011502378931140356111756932712822516814023166068902569458299933391973504078898958921809723346229893913662577294963528318424676803942288386430172430880307619748186863890050113934573820505570928109017842647598266634344447182347849367714564686341871007505886728393751147033556889217604647355628557502208364412269944908011305064122941446516990168924709684092200183860653173856272384
ce2 = 13908468332333567158469136439932325992349696889129103935400760239319454409539725389747059213835238373047899198211128689374049729578146875309231962936554403287882999967840346216695208424582739777034261079550395918048421086843927009452479936045850799096750074359160775182238980989229190157551197830879877097703347301072427149474991803868325769967332356950863518504965486565464059770451458557744949735282131727956056279292800694203866167270268988437389945703117070604488999247750139568614939965885211276821987586882908159585863514561191905040244967655444219603287214405014887994238259270716355378069726760953320025828158
tmp = 864078778078609835167779565982540757684070450697854309005171742813414963447462554999012718960925081621571487444725528982424037419052194840720949809891134854871222612682162490991065015935449289960707882463387
n = 15911581555796798614711625288508309704791837516232122410440958830726078821069050404012820896260071751380436992710638364294658173571101596931605797509712839622479368850251206419748090059752427303611760004621378226431226983665746837779056271530181865648115862947527212787824629516204832313026456390047768174765687040950636530480549014401279054346098030395100387004111574278813749630986724706263655166289586230453975953773791945408589484679371854113457758157492241225180907090235116325034822993748409011554673180494306003272836905082473475046277554085737627846557240367696214081276345071055578169299060706794192776825039
assert(pow(e1,ee1,n)==ce1)
assert(pow(e2+tmp,ee2,n)==ce2)
加密指数ee1和ee2都比较小,可以直接通过爆破得到e1和e2,脚本如下:
import gmpy2
def de(c, e, n):
k = 0
while True:
m,f= gmpy2.iroot(c + k*n, e)# 两个返回值,第二个返回值代表能否完全开方
if f:
return m
exit(0)
k += 1
e1 = de(ce1, ee1, n)
e2 = de(ce2, ee2, n) - tmp
print('e1=%s\ne2=%s'%(e1,e2))e1=15218928658178
e2=381791429275130第三部分
1
2
3
4
5
6
7
e = 46531
n = 16278524034278364842964386062476113517067911891699789991355982121084973951738324063305190630865511554888330215827724887964565979607808294168282995825864982603759381323048907814961279012375346497781046417204954101076457350988751188332353062731641153547102721113593787978587135707313755661153376485647168543680503160420091693269984008764444291289486805840439906620313162344057956594836197521501755378387944609246120662335790110901623740990451586621846212047950084207251595169141015645449217847180683357626383565631317253913942886396494396189837432429078251573229378917400841832190737518763297323901586866664595327850603
c = 14992132140996160330967307558503117255626925777426611978518339050671013041490724616892634911030918360867974894371539160853827180596100892180735770688723270765387697604426715670445270819626709364566478781273676115921657967761494619448095207169386364541164659123273236874649888236433399127407801843412677293516986398190165291102109310458304626261648346825196743539220198199366711858135271877662410355585767124059539217274691606825103355310348607611233052725805236763220343249873849646219850954945346791015858261715967952461021650307307454434510851869862964236227932964442289459508441345652423088404453536608812799355469
hint = int ( binascii . hexlify ( hint ), 16 )
assert ( q1p * q1q == n )
assert ( q1p < q1q )
assert ( c == pow ( hint , e , n ))
分解n,得到q1p=127587319253436643569312142058559706815497211661083866592534217079310497260365307426095661281103710042392775453866174657404985539066741684196020137840472950102380232067786400322600902938984916355631714439668326671310160916766472897536055371474076089779472372913037040153356437528808922911484049460342088834871求解得到hint,orz…you.found.me.but.sorry.no.hint…keep.on.and.enjoy.it!,没什么用,继续往下看。
1
2
3
4
5
6
7
flag = int ( binascii . hexlify ( flag ), 16 )
q1 = q1p
q2 = 114401188227479584680884046151299704656920536168767132916589182357583461053336386996123783294932566567773695426689447410311969456458574731187512974868297092638677515283584994416382872450167046416573472658841627690987228528798356894803559278308702635288537653192098514966089168123710854679638671424978221959513
c1 = 262739975753930281690942784321252339035906196846340713237510382364557685379543498765074448825799342194332681181129770046075018122033421983227887719610112028230603166527303021036386350781414447347150383783816869784006598225583375458609586450854602862569022571672049158809874763812834044257419199631217527367046624888837755311215081173386523806086783266198390289097231168172692326653657393522561741947951887577156666663584249108899327053951891486355179939770150550995812478327735917006194574412518819299303783243886962455399783601229227718787081785391010424030509937403600351414176138124705168002288620664809270046124
c2 = 7395591129228876649030819616685821899204832684995757724924450812977470787822266387122334722132760470911599176362617225218345404468270014548817267727669872896838106451520392806497466576907063295603746660003188440170919490157250829308173310715318925771643105064882620746171266499859049038016902162599261409050907140823352990750298239508355767238575709803167676810456559665476121149766947851911064706646506705397091626648713684511780456955453552020460909638016134124590438425738826828694773960514221910109473941451471431637903182205738738109429736425025621308300895473186381826756650667842656050416299166317372707709596
assert ( c1 == pow ( flag , e1 , p * q1 ))
assert ( c2 == pow ( flag , e2 , p * q2 ))
但是e与φ(n1), φ(n2)都不互素,公约数都为14,参考https://www.codenong.com/cs109681910/
def CRT(r,d):
M = 1
l = len(r)
for i in range(0,l):
M = d[i] * M
x = 0
for i in range(0,l):
md = M//d[i]
x = (x + gmpy2.invert(md, d[i]) * md *r[i] )%M
return int(M+x% M)%M
n1 = p * q1
n2 = p * q2
phi1 = (p-1)*(q1-1)
phi2 = (p-1)*(q2-1)
d1 = gmpy2.invert(e1//14,phi1)
d2 = gmpy2.invert(e2//14,phi2)
listq=[q1,q2]
lista=[]
a1 = gmpy2.powmod(c1,d1,n1)%q1
a2 = gmpy2.powmod(c2,d2,n2)%q2
lista.append(a1)
lista.append(a2)
last = CRT(lista,listq)
new_e = 7
new_phi = (q1-1)*(q2-1)
new_d = gmpy2.invert(new_e,new_phi)
m = gmpy2.powmod(last,new_d,q1*q2)
flag = gmpy2.iroot(m,2)[0]
print(binascii.unhexlify(hex(flag)[2:]))0x03 [QCTF2018]Xman-RSA
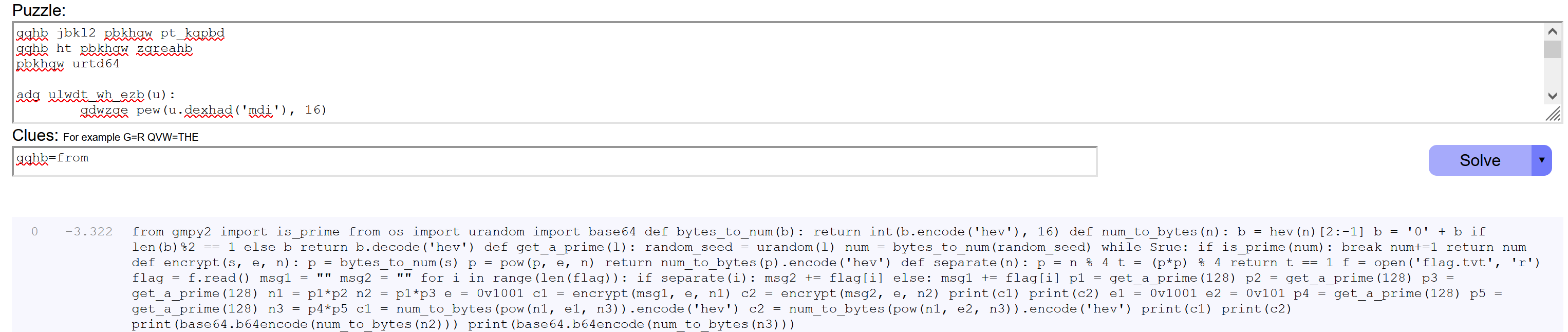
打开加密脚本,发现字符被替换掉了,这里用quipqiup进行词频分析后替换,再手动替换一些字符
from gmpy2 import is_prime
from os import urandom
import base64
def bytes_to_num(b):
return int(b.encode('hex'), 16)
def num_to_bytes(n):
b = hex(n)[2:-1]
b = '0' + b if len(b)%2 == 1 else b
return b.decode('hex')
def get_a_prime(l):
random_seed = urandom(l)
num = bytes_to_num(random_seed)
while True:
if is_prime(num):
break
num+=1
return num
def encrypt(s, e, n):
p = bytes_to_num(s)
p = pow(p, e, n)
return num_to_bytes(p).encode('hex')
def separate(n):
p = n % 4
t = (p * p) % 4
return t == 1
f = open('flag.txt', 'r')
flag = f.read()
msg1 = ""
msg2 = ""
for i in range(len(flag)):
if separate(i):
msg2 += flag[i]
else:
msg1 += flag[i]
p1 = get_a_prime(128)
p2 = get_a_prime(128)
p3 = get_a_prime(128)
n1 = p1*p2
n2 = p1*p3
e = 0x1001
c1 = encrypt(msg1, e, n1)
c2 = encrypt(msg2, e, n2)
print(c1)
print(c2)
e1 = 0x1001
e2 = 0x101
p4 = get_a_prime(128)
p5 = get_a_prime(128)
n3 = p4 * p5
c1 = num_to_bytes(pow(n1, e1, n3)).encode('hex')
c2 = num_to_bytes(pow(n1, e2, n3)).encode('hex')
print(c1)
print(c2)
print(base64.b64encode(num_to_bytes(n2)))
print(base64.b64encode(num_to_bytes(n3)))先用共模攻击把n1的值求出来2499586809914462821807624371088011200618603528498132509598946284572455726453497171635086810524607288333625665025664872216634366700044105279185519761587818169021167370991396691510275499486673922916370294043072503635630922980240462022218565365191228535222150496387990987123639567257124081274667568443678527637259644488779394704508217357758791670308548246801142468699716221789070607334747835552167450340441488756779323653879402176647890584656379628685893686585469918686253137796663587854943386347039389769790329948165162483370187914412810153613198247569427480466488647563900948387020677830797976534568626241686906738179
然后再通过gcd(n1,n2),得到p1的值68475150402136550069561649755295544963289030785101058202360554598728892273874900512013972536010281921862638482624050145776516868431210229550944533343142576416459199101144902197593841367980791503251475193609136925280837184839979646652186999511796418448787979170775450657311911945185202715164053596280658868979
然后求出p2和p3,进而求出m1、m2,利用下列脚本,求出flag
length = len(m1) + len(m2)
flag = ''
temp1 = 0
temp2 = 0
def separate(n):
p = n % 4
t = (p * p) % 4
return t == 1
for i in range(length):
if separate(i):
flag += m2[temp2]
temp2 = temp2 + 1
else:
flag += m1[temp1]
temp1 = temp1 + 1
print(flag)0x04 [INSHack2017]rsa16m
描述文件如下:
当您需要真正安全的通信时,可以使用带有4096位密钥的RSA。
我想要真正安全的通信来传输核发射代码(是的,IoT无处不在),
所以我使用了带有16777216位密钥的RSA。俄罗斯人肯定无法考虑这一点!
文件md5:1049a0c83a2e34760363b4ad9778753f题目给出了n、c、e的值,其中n和c的值非常非常大,相对而言,e的值很小,所以很有可能me 还是比n小,于是可以直接尝试对c开e次方。
data = open('rsa_16m', 'r')
n = data.readline()[4:]
c = data.readline()[4:]
c = int(c,16)
e = 0x10001
m = gmpy2.iroot(c,e)[0]
print(long_to_bytes(m).decode())0x05 [watevrCTF 2019]Swedish RSA
flag = bytearray(raw_input())
flag = list(flag)
length = len(flag)
bits = 16
## Prime for Finite Field.
p = random_prime(2^bits-1, False, 2^(bits-1))
file_out = open("downloads/polynomial_rsa.txt", "w")
file_out.write("Prime: " + str(p) + "\n")
## Univariate Polynomial Ring in y over Finite Field of size p
R.<y> = PolynomialRing(GF(p))
## Analogous to the primes in Z
def gen_irreducable_poly(deg):
while True:
out = R.random_element(degree=deg)
if out.is_irreducible():
return out
## Polynomial "primes"
P = gen_irreducable_poly(ZZ.random_element(length, 2*length))
Q = gen_irreducable_poly(ZZ.random_element(length, 2*length))
## Public exponent key
e = 65537
## Modulus
N = P*Q
file_out.write("Modulus: " + str(N) + "\n")
## Univariate Quotient Polynomial Ring in x over Finite Field of size 659 with modulus N(x)
S.<x> = R.quotient(N)
## Encrypt
m = S(flag)
c = m^e
file_out.write("Ciphertext: " + str(c))
file_out.close()输出给了三个量,一个是多项式素数最大值,一个是模数多项式,一个是密文多项式。首先分解Modulus
R.<y> = PolynomialRing(GF(43753))
N = R("34036*y^177 + ... + 23814")
factor(N)得到两个多项式
1
2
3
(34036)
* (y^65 + 39688*y^64 + 22199*y^63 + 41942*y^62 + 7803*y^61 + 19710*y^60 + 14794*y^59 + 41388*y^58 + 2418*y^57 + 19208*y^56 + 39941*y^55 + 36392*y^54 + 19813*y^53 + 33864*y^52 + 29099*y^51 + 15484*y^50 + 27185*y^49 + 27721*y^48 + 31508*y^47 + 19404*y^46 + 10134*y^45 + 43481*y^44 + 3899*y^43 + 32849*y^42 + 3534*y^41 + 32086*y^40 + 14221*y^39 + 42982*y^38 + 1403*y^37 + 1619*y^36 + 36054*y^35 + 33615*y^34 + 6628*y^33 + 31709*y^32 + 6968*y^31 + 28517*y^30 + 12938*y^29 + 21124*y^28 + 10400*y^27 + 28889*y^26 + 7273*y^25 + 36442*y^24 + 14935*y^23 + 29365*y^22 + 4869*y^21 + 43562*y^20 + 6435*y^19 + 4403*y^18 + 32311*y^17 + 7575*y^16 + 28199*y^15 + 28065*y^14 + 23870*y^13 + 37314*y^12 + 15299*y^11 + 7082*y^10 + 36230*y^9 + 18367*y^8 + 12531*y^7 + 25906*y^6 + 26878*y^5 + 43073*y^4 + 11582*y^3 + 4482*y^2 + 35044*y + 31388)
* (y^112 + 31097*y^111 + 15815*y^110 + 17170*y^109 + 43684*y^108 + 16873*y^107 + 17269*y^106 + 10853*y^105 + 10690*y^104 + 24864*y^103 + 10224*y^102 + 28704*y^101 + 16049*y^100 + 1154*y^99 + 40034*y^98 + 29922*y^97 + 27404*y^96 + 32514*y^95 + 40962*y^94 + 32858*y^93 + 36590*y^92 + 41302*y^91 + 20803*y^90 + 43521*y^89 + 13746*y^88 + 19857*y^87 + 21539*y^86 + 36888*y^85 + 16032*y^84 + 35825*y^83 + 24705*y^82 + 31143*y^81 + 22088*y^80 + 6686*y^79 + 37947*y^78 + 5661*y^77 + 29405*y^76 + 36071*y^75 + 35492*y^74 + 28985*y^73 + 36015*y^72 + 24095*y^71 + 34920*y^70 + 6615*y^69 + 9606*y^68 + 4255*y^67 + 22981*y^66 + 3910*y^65 + 23897*y^64 + 22711*y^63 + 23350*y^62 + 7969*y^61 + 8558*y^60 + 8001*y^59 + 8431*y^58 + 3314*y^57 + 23364*y^56 + 39391*y^55 + 32722*y^54 + 2543*y^53 + 22196*y^52 + 24189*y^51 + 19420*y^50 + 10649*y^49 + 19070*y^48 + 23863*y^47 + 19597*y^46 + 39699*y^45 + 7620*y^44 + 25067*y^43 + 29912*y^42 + 14998*y^41 + 14492*y^40 + 31322*y^39 + 43145*y^38 + 32006*y^37 + 38976*y^36 + 32534*y^35 + 6972*y^34 + 37351*y^33 + 30104*y^32 + 6032*y^31 + 33729*y^30 + 27110*y^29 + 5268*y^28 + 2974*y^27 + 2985*y^26 + 31610*y^25 + 28364*y^24 + 34924*y^23 + 17414*y^22 + 28813*y^21 + 43680*y^20 + 32175*y^19 + 18248*y^18 + 25171*y^17 + 31185*y^16 + 30125*y^15 + 36836*y^14 + 7218*y^13 + 11292*y^12 + 31123*y^11 + 40360*y^10 + 34093*y^9 + 39606*y^8 + 2788*y^7 + 27277*y^6 + 21835*y^5 + 1331*y^4 + 32614*y^3 + 25020*y^2 + 20981*y + 12108)
求解d需要e和phi,参考https://xz.aliyun.com/t/4545 ,phi = (43753^65-1)*(43753^112-1)
d = inverse_mod(e, phi)
ans = R("1")
temp= C
while(True):
if(d % 2 == 1):
ans = (ans * temp) % N
d = d - 1
d = d / 2
temp = (temp * temp) % N
if(d == 0):
break
#快速幂
print (ans)结果多项式为
1
125*y^62 + 111*y^61 + 114*y^60 + 117*y^59 + 53*y^58 + 51*y^57 + 51*y^56 + 100*y^55 + 106*y^54 + 110*y^53 + 102*y^52 + 106*y^51 + 100*y^50 + 104*y^49 + 101*y^48 + 117*y^47 + 52*y^46 + 52*y^45 + 57*y^44 + 48*y^43 + 50*y^42 + 107*y^41 + 35*y^40 + 101*y^39 + 114*y^38 + 117*y^37 + 99*y^36 + 101*y^35 + 115*y^34 + 110*y^33 + 105*y^32 + 95*y^31 + 116*y^30 + 117*y^29 + 98*y^28 + 95*y^27 + 110*y^26 + 117*y^25 + 102*y^24 + 95*y^23 + 115*y^22 + 105*y^21 + 95*y^20 + 97*y^19 + 101*y^18 + 107*y^17 + 105*y^16 + 95*y^15 + 109*y^14 + 111*y^13 + 114*y^12 + 102*y^11 + 95*y^10 + 65*y^9 + 83*y^8 + 82*y^7 + 123*y^6 + 114*y^5 + 118*y^4 + 101*y^3 + 116*y^2 + 97*y + 119
提取系数后,转ascii,再逆转
1
125 111 114 117 53 51 51 100 106 110 102 106 100 104 101 117 52 52 57 48 50 107 35 101 114 117 99 101 115 110 105 95 116 117 98 95 110 117 102 95 115 105 95 97 101 107 105 95 109 111 114 102 95 65 83 82 123 114 118 101 116 97 119
0x06 [watevrCTF 2019]ECC-RSA
from fastecdsa.curve import P521 as Curve
from fastecdsa.point import Point
from Crypto.Util.number import bytes_to_long, isPrime
from os import urandom
from random import getrandbits
def gen_rsa_primes(G):
urand = bytes_to_long(urandom(521//8))
while True:
s = getrandbits(521) ^ urand
Q = s*G
if isPrime(Q.x) and isPrime(Q.y):
print("ECC Private key:", hex(s))
print("RSA primes:", hex(Q.x), hex(Q.y))
print("Modulo:", hex(Q.x * Q.y))
return (Q.x, Q.y)
flag = int.from_bytes(input(), byteorder="big")
ecc_p = Curve.p
a = Curve.a
b = Curve.b
Gx = Curve.gx
Gy = Curve.gy
G = Point(Gx, Gy, curve=Curve)
e = 0x10001
p, q = gen_rsa_primes(G)
n = p*q
file_out = open("downloads/ecc-rsa.txt", "w")
file_out.write("ECC Curve Prime: " + hex(ecc_p) + "\n")
file_out.write("Curve a: " + hex(a) + "\n")
file_out.write("Curve b: " + hex(b) + "\n")
file_out.write("Gx: " + hex(Gx) + "\n")
file_out.write("Gy: " + hex(Gy) + "\n")
file_out.write("e: " + hex(e) + "\n")
file_out.write("p * q: " + hex(n) + "\n")
c = pow(flag, e, n)
file_out.write("ciphertext: " + hex(c) + "\n")ECC 和 RSA 的混合加密,需要求解p、q的值,点(p,q)根据椭圆曲线方程的一般形式:y^2 = x^3 + a*x + b,转换为q^2=p^3+a*p+b(mod ecc_p),因为n = p * q,代入可得 p^2*q^2= p^2* p^3+ p^2* a*p+ p^2* b (mod ecc_p) ,n^2=p^5+a*p^3+b*p^2 (mod ecc_p) 。a、b、n、ecc_p都是已知的,求解过程如下:
ecc_p = ECC Curve Prime
a = Curve a
b = Curve b
n = p * q
R.<x>=Zmod(ecc_p)[]
f = x^5 + a*x^3 + b*x^2 - n^2
f.roots()得到结果,设置为poss_p
1
2
3
4
5
6
7
8
9
10
11
12
13
[( 6813140671672694477701511883397067876211159809088064490593325584756562268820329988116480298456252746748095410666300132267213094431909630229631434972416225885 ,
1 ),
( 4573744216059593260686660411936793507327994800883645562370166075007970317346237399760397301505506131100113886281839847419425482918932436139080837246914736557 ,
1 ),
( 1859314969084523636298100850823722544590555574470838518640063093117116629078281861281849586432508721074855657736668366212762253040197962779753163192386773060 ,
1 )]
for p in poss_p :
q = n // p
phi = ( p - 1 ) * ( q - 1 )
d = invert ( e , phi )
m = pow ( c , d , n )
print ( binascii . unhexlify ( hex ( m )[ 2 :]))
0x07 [GKCTF 2021]RRRRsa
from Crypto.Util.number import *
from gmpy2 import gcd
flag = b'xxxxxxxxxxxxx'
p = getPrime(512)
q = getPrime(512)
m = bytes_to_long(flag)
n = p*q
e = 65537
c = pow(m,e,n)
print('c={}'.format(c))
p1 = getPrime(512)
q1 = getPrime(512)
n1 = p1*q1
e1 = 65537
assert gcd(e1,(p1-1)*(q1-1)) == 1
c1 = pow(p,e1,n1)
print('n1={}'.format(n1))
print('c1={}'.format(c1))
hint1 = pow(2020 * p1 + q1, 202020, n1)
hint2 = pow(2021 * p1 + 212121, q1, n1)
print('hint1={}'.format(hint1))
print('hint2={}'.format(hint2))
p2 = getPrime(512)
q2 = getPrime(512)
n2 = p2*q2
e2 = 65537
assert gcd(e1,(p2-1)*(q2-1)) == 1
c2 = pow(q,e2,n2)
hint3 = pow(2020 * p2 + 2021 * q2, 202020, n2)
hint4 = pow(2021 * p2 + 2020 * q2, 212121, n2)
print('n2={}'.format(n2))
print('c2={}'.format(c2))
print('hint3={}'.format(hint3))
print('hint4={}'.format(hint4))首先,把hint1经过二项式定理处理下,hint1=(2020p1202020 +q1202020 )%n1= 2020p1202020 +k1*q1
hint2利用费马小定理处理,hint2%q1=2021p1+212121= 2021p1+212121+k2*q1。
设2020为a,2021为b,202020为x,212121为y
hint1bx =(a p1x +k1*q1)*bx -–-–① x ax =(b p1x +k*q1)*ax -—-②
q1=gcd( ② ①
hint3=(ap2x +b q2x )%n2
hint4=(bp2y +a q2y )%n2
hint3y =[(ap2)x y+(bq2)x y]%n2
hint4x = [(bp2)x y+(aq2)x y]%n2
bx*y hint3y %n2-–-–③ x y*hint4x %n2-–-–④
q2=gcd( ③ ④
a = 2020
b = 2021
x = 202020
y = 212121
res1 = pow(hint2-y,x,n1) * pow(a,x,n1) - hint1*pow(b,x,n1)
q1 = gcd(res1,n1)
p1 = n1//q1
res2 = pow(b,x*y,n2) * pow(hint3,y,n2) - pow(a,x*y,n2) * pow(hint4,x,n2)
q2 = gcd(res2,n2)
p2 = n2//q2
phi1 = (q1-1)*(p1-1)
phi2 = (q2-1)*(p2-1)
d2 = gmpy2.invert(e,phi2)
q = pow(c2,d2,n2)
d1 = gmpy2.invert(e,phi1)
p = pow(c1,d1,n1)
phi = (q-1)*(p-1)
d = gmpy2.invert(e,phi)
m = pow(c,d,p*q)
print(long_to_bytes(m))0x08 [INSHack2019]Yet Another RSA Challenge - Part 1
import subprocess
p = subprocess.check_output('openssl prime -generate -bits 2048 -hex')
q = subprocess.check_output('openssl prime -generate -bits 2048 -hex')
flag = int('INSA{REDACTED}'.encode('hex'), 16)
N = int(p,16) * int(q,16)
print N
print '0x'+p.replace('9F','FC')
print pow(flag,65537,N)p的字符串被替换了,其中FC可能是原本就是FC也可能是9F替换的,我们发现共有4个FC
简单爆破下即可求出p,从而解出flag
0x09 [INSHack2019]Yet Another RSA Chall -Part 2
1
2
3
4
5
6
7
8
9
import subprocess
p = subprocess . check_output ( 'openssl prime -generate -bits 2048 -hex' )
q = subprocess . check_output ( 'openssl prime -generate -bits 2048 -hex' )
flag = int ( 'INSA {REDACTED} ' . encode ( 'hex' ), 16 )
N = int ( p , 16 ) * int ( q , 16 )
print N
print '0x' + p . replace ( '12' , '8D' ) . replace ( '33' , 'D4' ) . replace ( '5E' , 'FF' ) . replace ( '09' , '95' ) . replace ( 'E4' , '38' ) . replace ( '6B' , '89' ) . replace ( '9E' , 'E0' ) . replace ( '59' , '3E' )
print pow ( flag , 65537 , N )
属于上一题的升级版,替换的字符多了很多,脚本来源:https://ctftime.org/writeup/15206
0x0A [NCTF2019]easyRSA
1
2
3
4
5
6
7
8
9
10
11
12
13
14
from flag import flag
e = 0x1337
p = 199138677823743837339927520157607820029746574557746549094921488292877226509198315016018919385259781238148402833316033634968163276198999279327827901879426429664674358844084491830543271625147280950273934405879341438429171453002453838897458102128836690385604150324972907981960626767679153125735677417397078196059
q = 112213695905472142415221444515326532320352429478341683352811183503269676555434601229013679319423878238944956830244386653674413411658696751173844443394608246716053086226910581400528167848306119179879115809778793093611381764939789057524575349501163689452810148280625226541609383166347879832134495444706697124741
n = p * q
assert ( flag . startswith ( 'NCTF' ))
m = int . from_bytes ( flag . encode (), 'big' )
assert ( m . bit_length () > 1337 )
c = pow ( m , e , n )
print ( c )
# 10562302690541901187975815594605242014385201583329309191736952454310803387032252007244962585846519762051885640856082157060593829013572592812958261432327975138581784360302599265408134332094134880789013207382277849503344042487389850373487656200657856862096900860792273206447552132458430989534820256156021128891296387414689693952047302604774923411425863612316726417214819110981605912408620996068520823370069362751149060142640529571400977787330956486849449005402750224992048562898004309319577192693315658275912449198365737965570035264841782399978307388920681068646219895287752359564029778568376881425070363592696751183359
gcd(e,phi)=e,按常规方法根本无法求出私钥d,官方writeup:http://yulige.top/?p=752#easyRSA909pt_2solvers 。
sage代码源自:https://blog.csdn.net/weixin_52446095/article/details/119518573?utm_medium=distribute.pc_aggpage_search_result.none-task-blog-2~aggregatepage~first_rank_ecpm_v1~rank_v31_ecpm-6-119518573.pc_agg_new_rank&utm_term=%5BNCTF2019%5DeasyRSA&spm=1000.2123.3001.4430
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
import random
import time
def cal_k(s, r):
R.<x> = PolynomialRing(GF(r))
f = x * s + 1
k = int(f.roots()[0][0])
print(k)
return k
# About 3 seconds to run
def AMM(o, r, q):
start = time.time()
print('\n----------------------------------------------------------------------------------')
print('Start to run Adleman-Manders-Miller Root Extraction Method')
print('Try to find one {:#x}th root of {} modulo {}'.format(r, o, q))
g = GF(q)
o = g(o)
p = g(random.randint(1, q))
while p ^ ((q-1) // r) == 1:
p = g(random.randint(1, q))
print('[+] Find p:{}'.format(p))
t = 0
s = q - 1
while s % r == 0:
t += 1
s = s // r
print('[+] Find s:{}, t:{}'.format(s, t))
k = cal_k(s, r)
alp = (k * s + 1) // r
print('[+] Find alp:{}'.format(alp))
a = p ^ (r**(t-1) * s)
b = o ^ (r*alp - 1)
c = p ^ s
h = 1
for i in range(1, t):
d = b ^ (r^(t-1-i))
if d == 1:
j = 0
else:
print('[+] Calculating DLP...')
j = - dicreat_log(a, d)
print('[+] Finish DLP...')
b = b * (c^r)^j
h = h * c^j
c = c ^ r
result = o^alp * h
end = time.time()
print("Finished in {} seconds.".format(end - start))
print('Find one solution: {}'.format(result))
return result
def findAllPRoot(p, e):
print("Start to find all the Primitive {:#x}th root of 1 modulo {}.".format(e, p))
start = time.time()
proot = set()
while len(proot) < e:
proot.add(pow(random.randint(2, p-1), (p-1)//e, p))
end = time.time()
print("Finished in {} seconds.".format(end - start))
return proot
def findAllSolutions(mp, proot, cp, p):
print("Start to find all the {:#x}th root of {} modulo {}.".format(e, cp, p))
start = time.time()
all_mp = set()
for root in proot:
mp2 = mp * root % p
assert(pow(mp2, e, p) == cp)
all_mp.add(mp2)
end = time.time()
print("Finished in {} seconds.".format(end - start))
return all_mp
c = 10562302690541901187975815594605242014385201583329309191736952454310803387032252007244962585846519762051885640856082157060593829013572592812958261432327975138581784360302599265408134332094134880789013207382277849503344042487389850373487656200657856862096900860792273206447552132458430989534820256156021128891296387414689693952047302604774923411425863612316726417214819110981605912408620996068520823370069362751149060142640529571400977787330956486849449005402750224992048562898004309319577192693315658275912449198365737965570035264841782399978307388920681068646219895287752359564029778568376881425070363592696751183359
p = 199138677823743837339927520157607820029746574557746549094921488292877226509198315016018919385259781238148402833316033634968163276198999279327827901879426429664674358844084491830543271625147280950273934405879341438429171453002453838897458102128836690385604150324972907981960626767679153125735677417397078196059
q = 112213695905472142415221444515326532320352429478341683352811183503269676555434601229013679319423878238944956830244386653674413411658696751173844443394608246716053086226910581400528167848306119179879115809778793093611381764939789057524575349501163689452810148280625226541609383166347879832134495444706697124741
e = 0x1337
cp = c % p
cq = c % q
mp = AMM(cp, e, p)
mq = AMM(cq, e, q)
p_proot = findAllPRoot(p, e)
q_proot = findAllPRoot(q, e)
mps = findAllSolutions(mp, p_proot, cp, p)
mqs = findAllSolutions(mq, q_proot, cq, q)
print(mps, mqs)
def check(m):
h = m.hex()
if len(h) & 1:
return False
if bytes.fromhex(h).startswith(b'NCTF'):
print(bytes.fromhex(h))
return True
else:
return False
# About 16 mins to run 0x1337^2 == 24196561 times CRT
start = time.time()
result = []
print('Start CRT...')
for mpp in mps:
for mqq in mqs:
solution = CRT_list([int(mpp), int(mqq)], [p, q])
if check(solution):
print(solution)
result.append(bytes.fromhex(solution.hex()))
print(time.time() - start)
end = time.time()
print("Finished in {} seconds.".format(end - start))
print("result:", result)
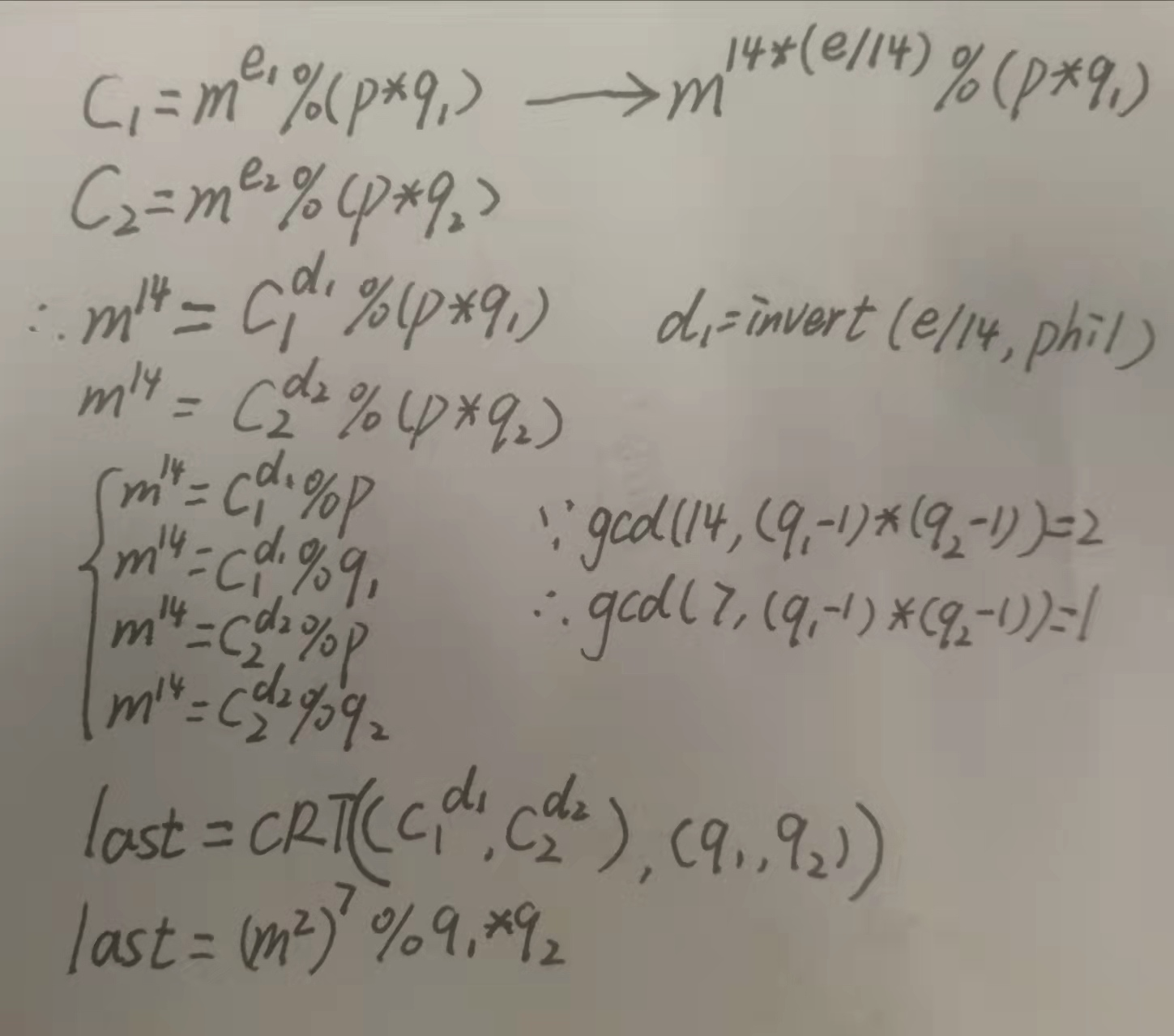


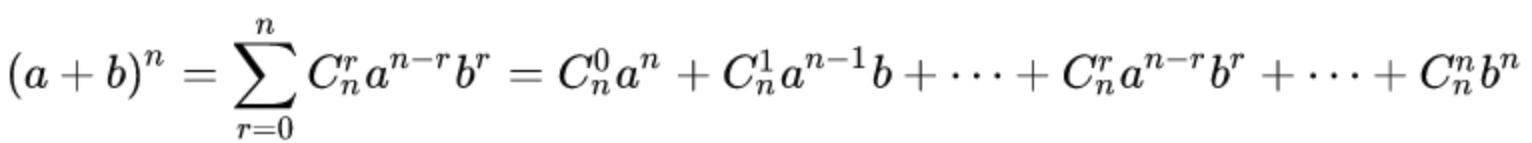
![]()

